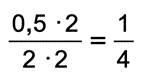”Att vända den sista bråkdelen upp och ner” eller ”att räkna diagonalt” ger liten förståelse. I den här artikeln kommer Kikora att beskriva en alternativ lösningsstrategi som kan ge eleverna en djupare förståelse för bråkräkning.
Ett exempel från klassrummet
”Finns det problem med det här sättet att dividera bråk?”

Så här startar diskussionen i ett forum för matematiklärare. Elevens tillvägagångssätt är som följer:
- Först delar eleven täljare med täljare och nämnare med nämnare:
- Därefter löser eleven divisionerna:
- Slutligen förlänger eleven bråket, för att undvika decimaltal i täljaren:
- Eleven drar slutsatsen att svaret är en fjärdedel:
Utifrån insikt i detta skriftliga svar är det omöjligt att svara på om elevens alternativa lösningsstrategi gav ett bättre läranderesultat och en djupare förståelse. Eleven kanske hade tur? Det vi ser är att eleven bryter sig ur de ”vanliga” och dominerande metoderna.
Metod 1: Vänd det sista bråket och byt till multiplikation.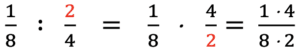
Metod 2: Byt diagonalt.

De två ovan nämnda strategierna fungerar effektivt. Om de ger förståelse är mer osäkert. När du vänder på den sista bråkdelen och byter från att dividera till att multiplicera, handlar det plötsligt inte om att dividera längre. När eleven frågar: ”Vilket bråk ska jag konvertera?” signalerar detta att dessa strategier är instrumentella. Eleven följer ett recept. Är detta ett farligt förhållningssätt inför ett matematiskt problem?
En strategi som är vettig
I exemplet ovan har eleven utforskat och upptäckt en strategi – vilket går helt i linje med den uppdaterade läroplanen, Lgr22. Eleverna ska erbjudas möjligheten att just utforska olika strategier, som ett led i att utveckla en självständighet och tilltro till den egna matematiska förmågan.
Förmågan att självständigt lösa matematiska frågeställningar och reflektera över de val man gör. Det är en bärande komponent som genomsyrar matematikämnet genom hela grundskolan; Tillåt eleverna vara aktiva och interagera med matematiken.
Elever ska utbildas i att välja lämpliga metoder och strategier, men vad är egentligen lämplig metod och strategi? Är det att välja kortaste och snabbaste väg till svaret, kommer vi också välja att använda en begränsad del av hjärnan. Är det istället att eleven använder sig av strategier som utmanar en större kapacitet för lärande, genom att utveckla förståelse och djupinlärning – behöver vi erbjuda fler, och andra, vägar.
Kikora har skapat ett läropaket där eleven delar bråk med hjälp av gemensamma nämnare. Detta bryter med de traditionella instrumentella strategierna när man hanterar bråk.

Strategin kan ge eleven en ökad förståelse för vad man faktiskt gör: man delar ett värde med ett annat värde. Visualiseringarna kan bidra till att göra värdet av de olika bråken mer påtagliga, förutom att understryka att täljaren i det första bråket måste delas – ”täcka” – täljaren i det andra bråket ett visst antal gånger – och så att denna kan göras direkt måste bråken vara ”av samma sort”, dvs ha samma nämnare.
Introduktionen i läropaketet aktiverar nödvändiga förkunskaper:

I arbetet med denna strategi är det nödvändigt att eleven har förstått konceptet att expandera och förkorta bråk, samt kunna jämföra värden på olika bråk. .
Utbildningen är då differentierad. Eleven väljer en inlärningsstig i ökande svårighetsgrad: Stig A, B eller C. Till att börja med möter eleverna bråk med gemensamma nämnare. Gradvis under inlärningsprocessen måste eleverna förlänga eller förkorta bråk till gemensamma nämnare.

Efter introduktionen bygger eleverna upp sin förståelse genom att utföra olika uppgifter. Här är några exempel:
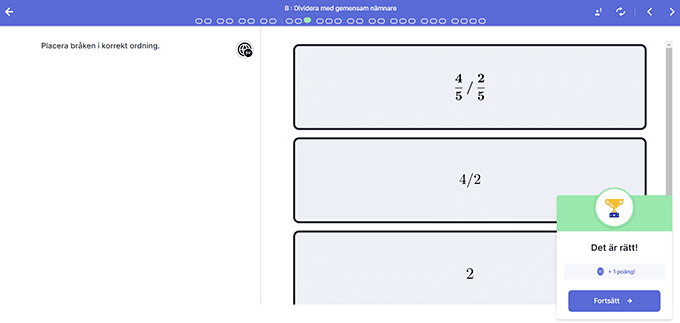
Så småningom är tanken att eleven ska upptäcka att om nämnarna är olika kan man förlänga eller förkorta dem så att de blir lika, och sedan ställa frågan hur mycket den första kan täcka den andra.
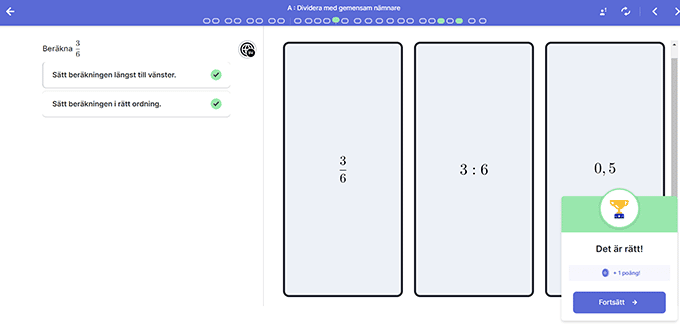
Läropaketet innehåller även uppgifter där eleven ska lösa uppgifter utan stöd av illustrationer. Då nyttjar man vår inbyggda Mattemotor aktivt och får feedback på delberäkningar längs vägen:

Med detta läropaket hoppas vi på Kikora bidra till en ökad förståelse för vad som faktiskt händer när man dividerar med bråk: man delar ett värde med ett annat värde.